Control of Chaotic Flows and Fluid Forces (Previous Part)
Perturbation Expansion
The distribution function may be expanded as a multiscale perturbation expansion in terms of a small parameter ![]() as follows:
as follows:
![]()
The second component of the multiscale perturbation expansion of ![]() is not a second order derivative; it simply indicates the expansion of the time scale in the second position.
is not a second order derivative; it simply indicates the expansion of the time scale in the second position.
![]()
and ![]() .
.
Using the above expansions in Eq. (??), we obtained
(1) 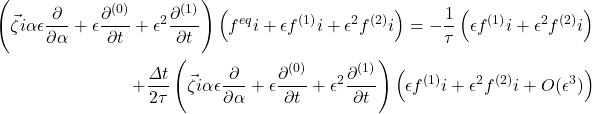
Control of Chaotic Flows and Fluid Forces Around Two Offset Cylinders in Presence of Control Plate (Part 2)
Equating coefficient of ![]()
(2) ![]()
O(![]() ):
):
(3) 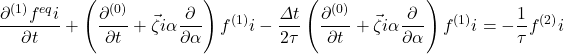
Moments and Recombination
Zeroth Moment
To find zeroth moment of Eq. (2) of O(![]() ) sum the equation over
) sum the equation over ![]()
(4) 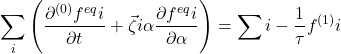
(5) ![]()
Distribution function is written as
![]()
By adding the above equation over ![]() , we get
, we get
(6) ![]()
Since ![]() , and
, and
![]()
By adding the above equation over ![]() , we get
, we get
![]()
Since the sum of weight factor is always equal to one i.e. ![]() . Therefore from above equation we get
. Therefore from above equation we get
![]()
Using above equation in Eq. (6), we get
![]()
From above equation, we get
![]()
![]()
So Eq. (5) becomes
(7) ![]()
First Moment
To find zeroth moment of Eq. (2) of O(![]() ) we multiply this equation with
) we multiply this equation with ![]() and sum over \textit{i} and index changing to
and sum over \textit{i} and index changing to ![]()
![Rendered by QuickLaTeX.com \[\sum_{i}\left(\vec \zeta_{i\alpha} \frac{\partial^{(0)} f^{eq}_{i}}{\partial t}+\vec \zeta_{i\beta}\vec \zeta_{i\alpha}\frac{\partial f^{eq}_{i}}{\partial \beta}\right) = \sum_{i}-\frac{1}{\tau}\vec \zeta_{i\alpha}f^{(1)}_{i}\]](https://ranamaths.com/wp-content/ql-cache/quicklatex.com-102b6edb4a19d58a5efccf71f83d6dd2_l3.png)
(8) 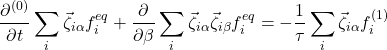
Since
![]()
So Eq. (8) becomes
(9) ![]()
Second Moment
To find zeroth moment of Eq. (2) of O(![]() ) we multiply this equation with
) we multiply this equation with ![]() and sum over \textit{i} and index changing to
and sum over \textit{i} and index changing to ![]()
![Rendered by QuickLaTeX.com \[\sum_{i}\left(\vec \zeta_{i\alpha}\vec \zeta_{i\beta} \frac{\partial^{(0)} f^{eq}_{i}}{\partial t}+\vec \zeta_{i\gamma}\vec \zeta_{i\beta}\vec \zeta_{i\alpha}\frac{\partial f^{eq}_{i}}{\partial \gamma}\right) = \sum_{i}-\frac{1}{\tau}\vec \zeta_{i\alpha}\vec \zeta_{i\beta}f^{(1)}_{i}\]](https://ranamaths.com/wp-content/ql-cache/quicklatex.com-99461b280a76b138b19958e1e182e321_l3.png)
(10) 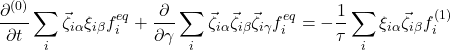
Since
![]()
So Eq. (10) becomes
(11) ![]()
Now we calculate the zeroth, and first moment of O(![]() ).
).
Zeroth Moment of O(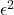 )
)
To find zeroth moment of Eq. (3) of O(![]() ) sum the equation over
) sum the equation over ![]()
![Rendered by QuickLaTeX.com \[\sum_{i}\left( \frac{\partial^{(1)} f^{eq}_{i}}{\partial t}+\left( \frac{\partial^{(0)}}{\partial t}+\vec \zeta_{i\alpha}\frac{\partial}{\partial \alpha} \right)f^{(1)}_{i} -\frac{\mathit{\Delta}t}{2\tau}\left( \frac{\partial^{(0)}}{\partial t}+\vec \zeta_{i\alpha}\frac{\partial}{\partial \alpha}\right)f^{(1)}_{i}\right) =-\sum_{i}\frac{1}{\tau}f^{(1)}_{i}\]](https://ranamaths.com/wp-content/ql-cache/quicklatex.com-9bf15958af1d7b805f8ad35a8567d77d_l3.png)
(12) 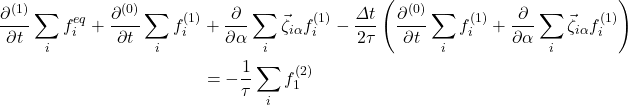
Now since,
![]()
So Eq. (12) becomes
(13) ![]()
First Moment of O(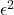 )
)
To find zeroth moment of Eq. (3) of O(![]() ) we multiply this equation with
) we multiply this equation with ![]() and sum over \textit{i} and index changing to
and sum over \textit{i} and index changing to ![]()
(14) 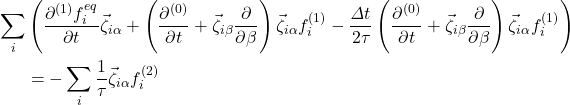
(15) 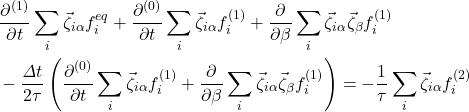
Now since,
![]()
So Eq. (15) becomes
(16) ![]()
Now by combining Eq. (7) and (13), we get
![Rendered by QuickLaTeX.com \[\epsilon\left(\frac{\partial^{(0)}\rho}{\partial t}+\frac{\partial(\rho u_{\alpha})}{\partial \alpha}\right)+\epsilon^{2}\left( \frac{\partial^{(1)} \rho}{\partial t} \right)=0 \]](https://ranamaths.com/wp-content/ql-cache/quicklatex.com-a42437fefa4b80414309f35a4b1ba8f4_l3.png)
![Rendered by QuickLaTeX.com \[\left( \epsilon\frac{\partial^{(0)}}{\partial t}+\epsilon^{2}\frac{\partial^{(1)}}{\partial t}\right)\rho+ \epsilon \frac{\partial(\rho u_{\alpha})}{\partial \alpha}=0\]](https://ranamaths.com/wp-content/ql-cache/quicklatex.com-ed6b9f5c7e32a0e32018b821083dda61_l3.png)
Control of Chaotic Flows and Fluid Forces (Previous Part)

Very knowledgeable
Hello! I hope you’re having a great day. Good luck 🙂