Control of Chaotic Flows and Fluid Forces (Previous Part 3)
![]()
Using these results in above equation we get the mass conservation
(1) ![]()
Now by combining Eq. (??) and (??), we get
![Rendered by QuickLaTeX.com \[\epsilon\left(\frac{\partial^{(0)}(\rho u_{\alpha})}{\partial t}+\frac{\partial (\Pi^{eq}_{\alpha \beta})}{\partial \beta} \right)+\epsilon^{2}\left(\frac{\partial^{(1)}}{\partial t}\left(\rho u_{\alpha} \right)+\frac{\partial}{\partial \beta}\left(1-\frac{\mathit{\Delta}t}{2\tau} \right)\Pi^{1}_{\alpha \beta}\right)=0\]](https://ranamaths.com/wp-content/ql-cache/quicklatex.com-4aa2732e0bcb32631ff721b0b11ddd83_l3.png)
(2) 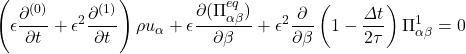
As
![]()
So Eq. (2) becomes
(3) ![]()
For D2Q9, we have the gas dynamical relation
![]()
Now by replacing ![]() by
by ![]() in above equation. We get
in above equation. We get
(4) ![]()
Let
(5) ![]()
(6) ![]()
Read Control of Chaotic Flows and Fluid Part 1
We use the relation for the tensor
![]()
So from Eq. (5) we have
![]()
Consider
(7) 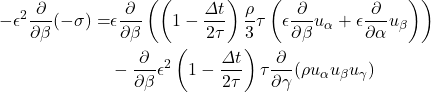
Let
![]()
![]()
So Eq. (7) becomes
(8) ![]()
Combining Eq. (6) and (8), we get
![]()
Here \textit{E} represent the error term, we neglect this to get quadratic Navier Stokes equation.
(9) ![]()
Consider the Navier stokes equation
![]()
Comparing above equation with Eq. (9), we get
![]()
Replacing ![]() with
with ![]() in Eq. (9) we get
in Eq. (9) we get
![]()
Above equation can also be represented as
![]()
![]() We concluded that in macroscopic limit LBE Recovers Navier-Stokes equations
We concluded that in macroscopic limit LBE Recovers Navier-Stokes equations
![]()
![]()
Boundary conditions in LBM
PDE solutions are unable to be determined uniquely without using proper initial and BCs. LBM does not allow for the application of BCs directly. It’s necessary to convert the BCs into streaming-in distribution functions. In LBM BCs Kruger ![]()
![]() ., there are two types of groups: lattice links and lattice nodes, referred to as link-wise and wet node, respectively.
., there are two types of groups: lattice links and lattice nodes, referred to as link-wise and wet node, respectively.
Convective boundary conditions
The convective BC’s are the linear combination of the function values, and its derivative at the computational domain boundary is a mixed form of BCs from some problems this boundary is also known as the impedance boundary.
The following is a mathematical representation of convective BCs.
(10) ![]()
Where ![]() is the uniform and
is the uniform and ![]() ,
, ![]() are in-flow velocity, such type of BC is used in the computational domain outlet, and the velocity is chosen in such a way that one can maintain general conservation.
are in-flow velocity, such type of BC is used in the computational domain outlet, and the velocity is chosen in such a way that one can maintain general conservation.
Lift coefficient
The lift coefficient is the proportion of lift produced by a lifting body to the fluid density around it.
(11) ![]()
where, ![]() is the lift force of body.
is the lift force of body.
Drag coefficient
The drag coefficient is an important tool for determining an object’s aerodynamic efficiency, regardless of its size or shape. The flow is streamline when the drag coefficient is low.
(12) ![]()
where, ![]() is the drag force of body and
is the drag force of body and ![]() is the density of fluid.
is the density of fluid.
Control of Chaotic Flows and Fluid Part 1
